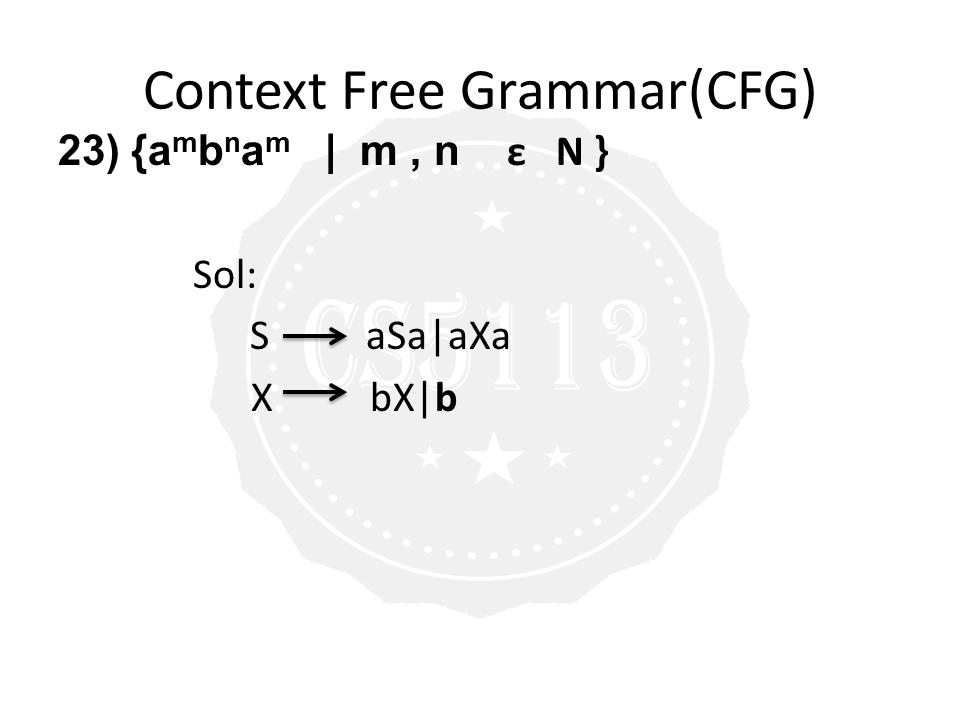
Context Free Grammar for {a^mb^na^m | m , n ε N } | CFG for {a^mb^na^m

Context Free Grammar for {a^mb^na^m | m , n ε N } | CFG for {a^mb^na^m | m , n ε N }

To construct a context-free grammar (CFG) for the language $L = {a^m b^n a^m mid m, n in mathbb{N}}$ , we need to ensure that:

CFG Construction

Start Symbol:

S

Production Rules:

Explanation of the Rules:

The rule $S rightarrow aSa$ allows us to add matching pairs of $a$ ‘s at the beginning and end of the string, recursively building the structure while ensuring the same number of $a$ ‘s at both ends.
The rule $S rightarrow B$ transitions to the non-terminal $B$ once all $a$ ‘s have been placed, so that we can handle the $b$ ‘s in the middle part of the string.

This rule generates any number of $b$ ‘s in the middle. The production $B rightarrow bB$ adds a $b$ to the middle part and recursively continues. The rule $B rightarrow epsilon$ allows for the middle part to have zero or more $b$ ‘s.

Example Derivations:

For $m = 2$ and $n = 3$ , the string $a^2 b^3 a^2$ would be generated as follows:

$S Rightarrow aSa Rightarrow aaSaa$
Next, we need to derive $S$ to $B$ :
- $S Rightarrow B$
- $B Rightarrow bB Rightarrow bbB Rightarrow bbbB Rightarrow bbbepsilon$
Combining these, we get: $aa , bbb , aa$

This CFG effectively generates all strings in the language ${a^m b^n a^m mid m, n in mathbb{N}}$ .