This course includes various topics, and you can find their complete details on our website.
LANGUAGES

- All String Languages
- Even Languages
- Odd Languages
- Prime Languages
- Language (Formal and Informal )
- Languages for Length Exactly Two
- Languages for Length at Least two
- Languages for Length at most Two
- Lexicographic order
Context Free Grammar (CFG)

- CFG) for ab*
- (CFG) for (ab)*
- (CFG) for a*b*
- (CFG) for b*a*
- (CFG) for (a + b)*
- (CFG) for a( a + b )*
- (CFG) for ( a + b )*ab
- (CFG) for (a+b)*aa(a+b)*
- (CFG) for a*+b*
- (CFG) for (a + ab)* + bb*
- (CFG) for ab* + b*
- (CFG) for {a^nb^n | n ε N }
- (CFG) for {a^nb^n | n ε W }
- (CFG) for {a^nb^nc^n | n ε N }
- (CFG) for {a^mb^n | m >n ε N }
- (CFG) for a^2nb^n
- (CFG) for {a^mb^n | m >n & m ,n =0,1,2,….}
- (CFG) for {a^mb^n | m < n & m ,n =0,1,2,….}
- (CFG) for a^mb^n
- (CFG) for {a^mb^n | m ≠ n & m ,n =0,1,2,….}
- (CFG) for {a^mb^nc^m+n | m ,n =0,1,2,….}
- (CFG) for {a^mb^mc^n | m , n ε N }
- (CFG) for {a^mb^nc^n | m , n ε N }
- (CFG) for {a^mb^na^m | m , n ε N }
- (CFG) for Equal Number of a’s and b’s
- (CFG) for Un-Equal Number of a’s and b’s
- (CFG) for Palindrome
- (CFG) for Non-Palindrome
- (CFG) for Language of All Palindrome(Even Length)
- (CFG) for Language of All Palindrome(Odd Length)
- (CFG) for Even String ((a+b)(a+b))*
Regular Expression(RE)
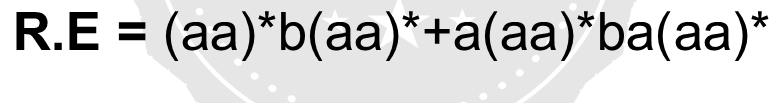
- Regular Expression for Language of all those strings which end with ‘aa’ or ‘ab’ and have odd length?
- Regular Expression for Language of all those strings which do not contain substring ‘bb’ ?
- Regular Expression for Language of all those strings whose length is odd and contain exectly one b ?
Finite State Automata(FSA)
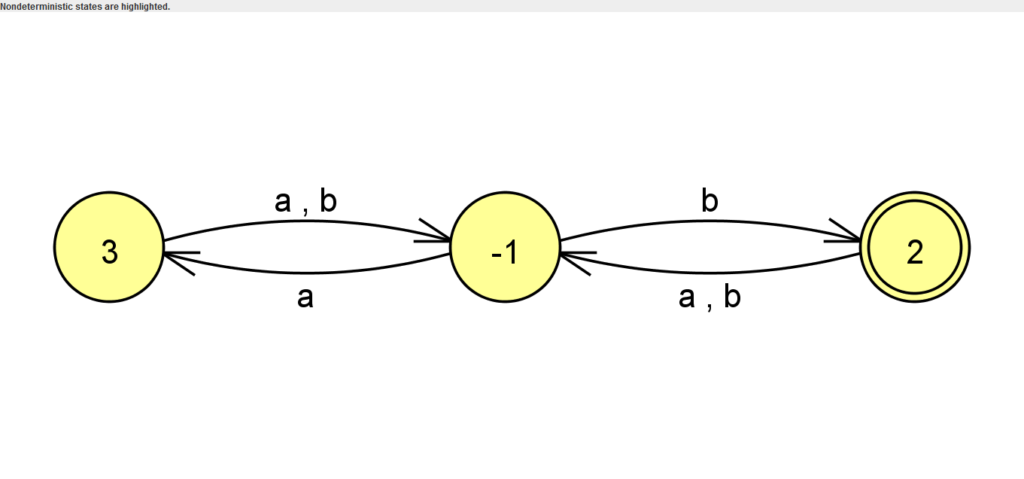
- FSA for End with “aa” or “ab” and have Odd length
- FSA for Don’t contain Substring “bb”
- FSA for Length is Odd and End with “b”
- FSA for String which have End with “b”
Push Down Automata(PDA)
- PDA for { a^mb^n / m > n ∈ N }
- PDA for { a^mb^n / m < n ∈ N }
- PDA for { a^mb^m+n c^n / m,n ∈ N }
- PDA for { a^mb^n c^m+n / m,n ∈ N }
- PDA for Even Palindrome
- PDA for Odd Palindrome
- PDA for Palindrome
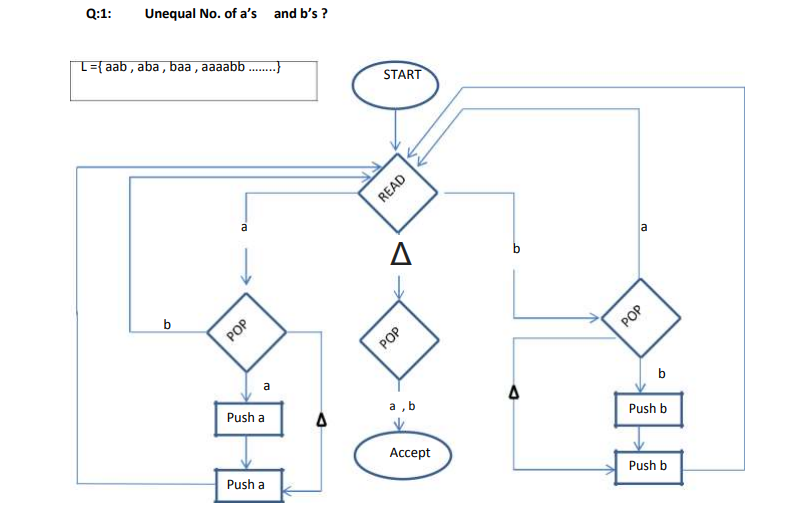
- PDA for UnEqual Number of a and b
Turing Machine (TM)
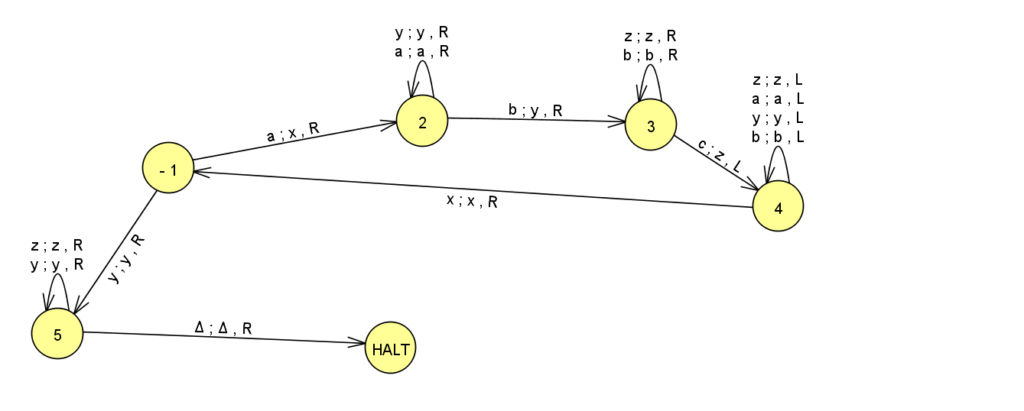
- Turing Machine for a^nb^n
- Turing Machine for a^nb^nc^n
- Turing Machine for a^mb^mc^nd^n
- Turing Machine for a^mb^nc^md^n
- Turing Machine for a^mb^n+mc^n
- Turing Machine for a^mb^nc^m+n
- Turing Machine for the language { b^na^kn | n= 0 , 1 , 2 …………} for k = 5
Palindrome & Non-Palindrome
- Turing Machine for Palindrome
- Turing Machine for Non-Palindrome
Equal & Un-Equal Number’s
- Turing Machine for Equal number of a’s and b’s
- Turing Machine for Un-Equal number of a’s and b’s
Replace
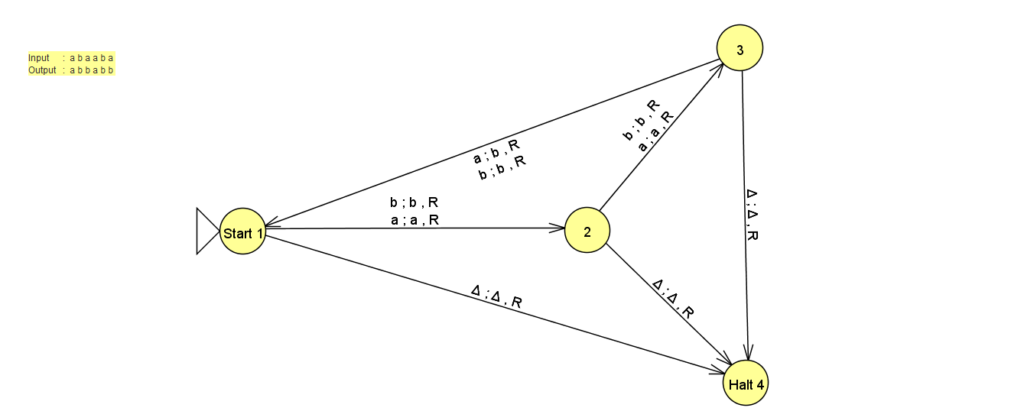
- Turing Machine(TM) for Odd length and Replace middle symbol with ‘x’
- Turing Machine(TM) for Replace Every Third symbol with ‘b’
Reverse String
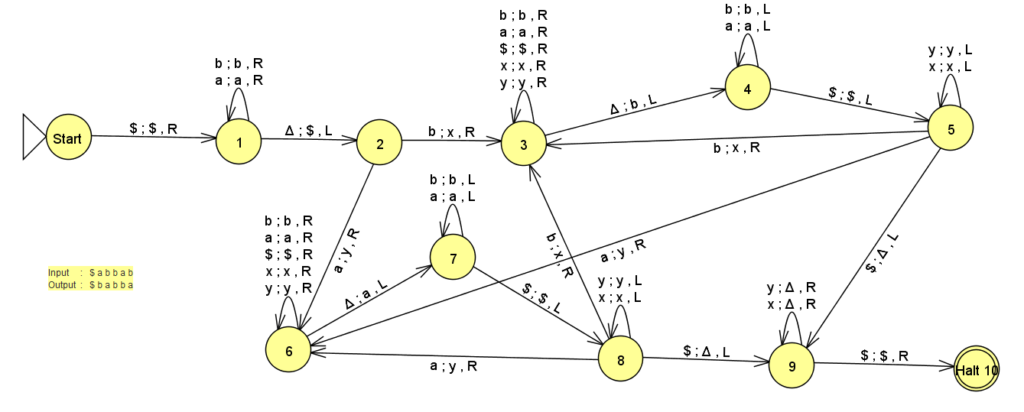
- Turing Machine for Reverse String ( First Method )
- Turing Machine for Reverse String ( Second Method )
Copy of String
- Turing Machine(TM) for Copy of String
Insert Position
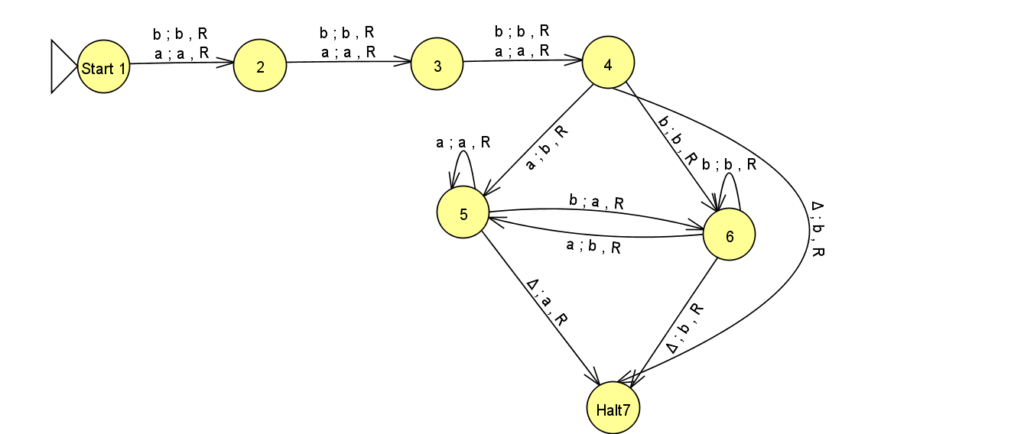
- Turing Machine (TM) for Insert ‘b’ at First Position
- Turing Machine(TM) for Insert ‘b’ at Fourth Position
- Turing Machine (TM) for Insert ‘b’ at Last Position
Delete Symbol’s
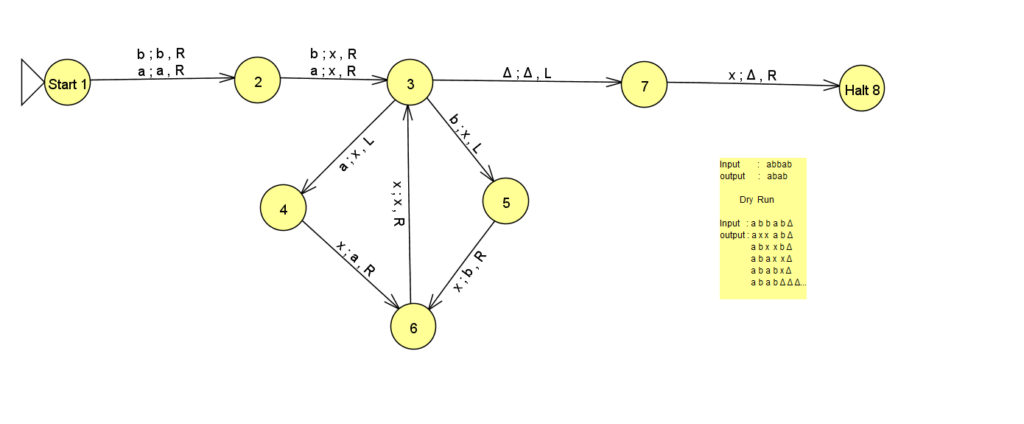
- Turing Machine(TM) for Delete First Symbol
- Turing Machine(TM) for Delete Second Symbol
- Turing Machine(TM) for Delete Second Last Symbol
- Turing Machine(TM) for Delete Third Symbol (First Method)
- Turing Machine(TM) for Delete Third Symbol (Second Method)
- Turing Machine(TM) for Delete Third Last Symbol
- Turing Machine(TM) for Delete Last Symbol